Table of Contents
What is probability theory?
Most phenomena in our lives are partially random. Think about weather forecasting, the stock market, and football game outcomes.
These are all things we can’t exactly predict, but fortunately, we can spot behaviors through probability theory.
Probability theory is a branch of statistics that studies random phenomena and their results.
What is a random experiment?
In statistics, a random experiment is an observable phenomenon whose result can’t be exactly predicted.
Random experiments are the rolling of a die, the tossing of a coin, the professor’s drawing for the oral test…
What is the sample space of an experiment?
In a random experiment, we don’t know exactly the outcome, but we know all the possible ones.
In probability theory, the set of possible outcomes of a random experiment is called the sample space.
The sample space is denoted by the Greek letter Ω (omega).
In a lot of situations, it’s also useful to know the number of elements of the sample space. This is called the “cardinality” and it’s written |Ω|.
Example of sample spaces
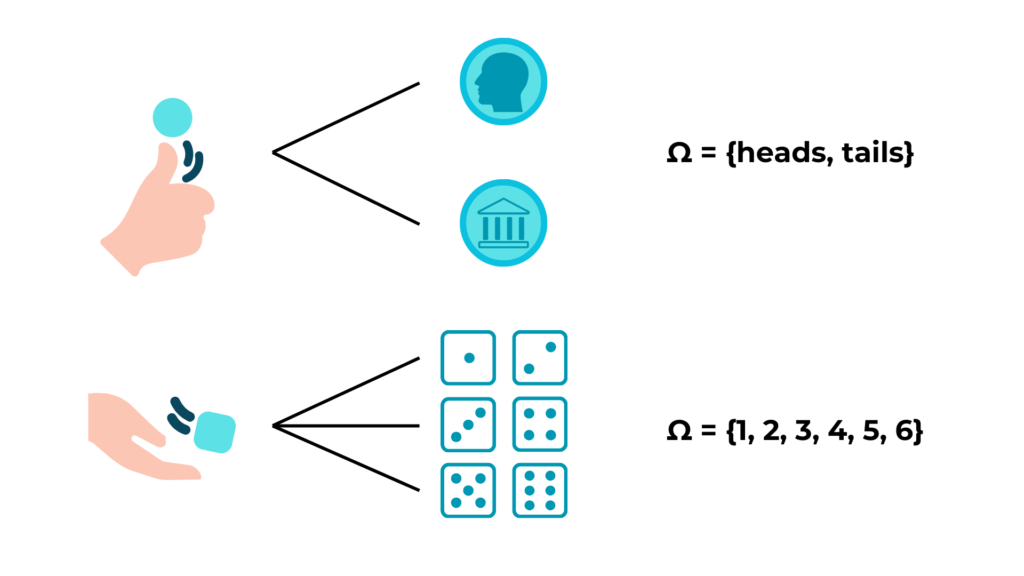
1) Identify the sample space when tossing a fair coin.
In a coin toss, presuming that the coin is fair, we have 2 possible outcomes: heads and tails.
So the sample space is:
Ω = {heads, tails}
|Ω| = 2
2) Identify the sample space when rolling a dice.
When we roll a normal dice, we have 6 possible outcomes: 1, 2, 3, 4, 5, 6.
What did I hear? “These are just the elements of the sample space”? You’re right!
Ω = {1, 2, 3, 4, 5, 6}
|Ω| = 6
What is an event?
A random event is a situation that occurs when the outcome of an experiment has certain characteristics.
We denote an event as a set of outcomes for which the following occurs.
E = {…}
Logically, an event is therefore a subset of the sample space.
Example of events
1) Identify the event that occurs when the outcome of a coin toss is tails.
In a coin toss, presuming that the coin is fair, we have 2 possible outcomes: heads and tails.
Ω = {heads, tails}
Our E is a subset of Ω that contains the outcome for which E occurs.
In this case, E occurs when the “output” is tails.
E = {tails}
2) Identify the event that occurs when the outcome of a dice roll is an even number.
When we roll a normal dice, we have 6 possible outcomes: 1, 2, 3, 4, 5, 6.
Ω = {1, 2, 3, 4, 5, 6}
E is a subset of Ω that contains all the even numbers of the sample space.
E = {2, 4, 6}