Definition of probability
Probability is a word that we use a lot in our everyday life.
Winning the lottery and being struck by lightning is very unprobable. Instead, receiving a notification on the phone or encountering traffic on the street are probable things in a day.
Its meaning in relativity theory is intuitive and isn’t different from the common use we make of the word.
Probability express the ease of realization of an event.
How do you get to the probability formula?
Problem statement
Let’s take a random experiment, like the roll of a dice. I’m trying to come up with a formula to calculate probability from common sense.
Now define 3 events:
- E1 = {6}. It occurs when the result is 6.
- E2 = {1, 2, 3, 4}. It occurs when the result is < 5.
- E3 = {1, 2, 3, 4, 5, 6}. It occurs for every possible output.
We would say that E1 is improbable, E2 is probable, and E3 is certain.
Observations
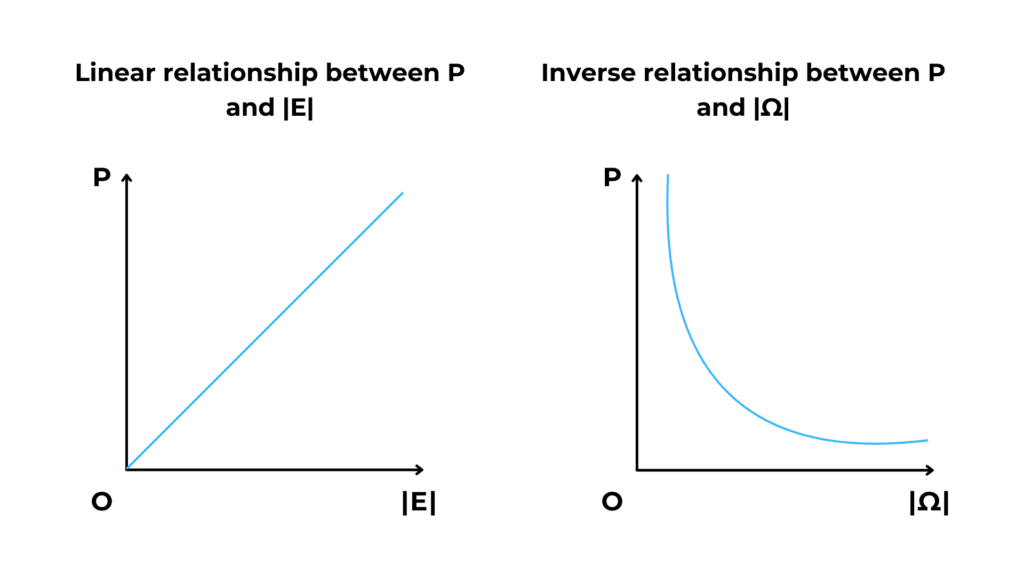
The probability we logically associate to an event depends on 2 variables, the number of favorite outcomes ( |E| ) and the number of possible outcomes ( |Ω| ).
We notice that as |E| increases the probability increases, so they have a linear relationship.
Opposite, when |Ω| increases the probability decreases, so they have an inverse relationship.
That’s it! Now we must write our observations using math.
Classic probability formula
The formula for calculating the probability P(E) of a random event E is:
In more sophisticated terms:
When can’t we use this formula?
Different probable cases
Imagine a random experiment in which I have to box against Mike Tyson, and an event E comes true if I win.
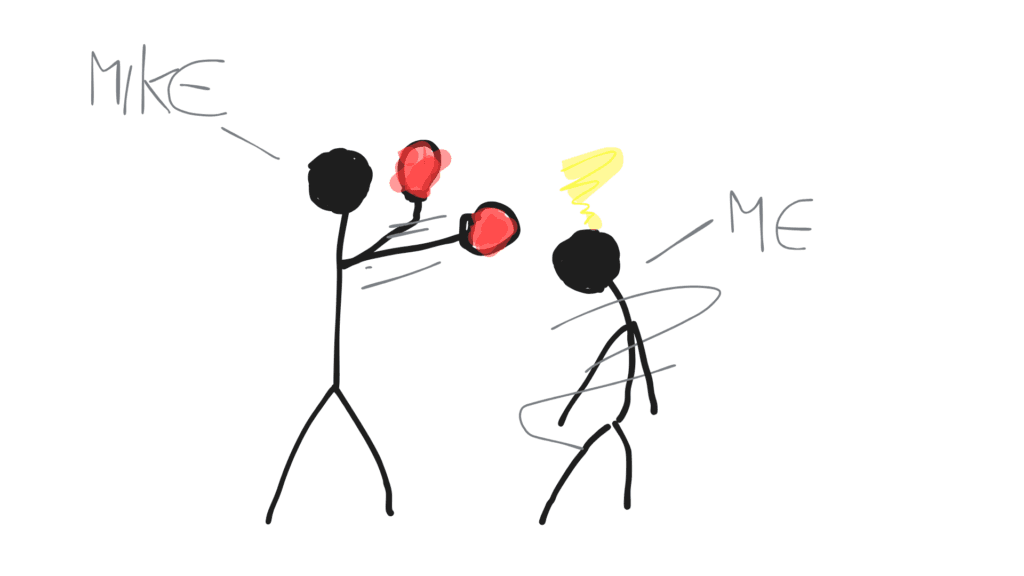
The number of possible cases is 2; either I win or lose. The favorable case is 1, the one in which I win.
So:
Formally our result is right, but intuitively it is not.
The classic probability formula doesn’t help when the single cases of a random experiment aren’t equally likely to happen.
Infinite sets
Let’s randomly pick a natural number, and let E be an event that occurs when the outcome is an even number.
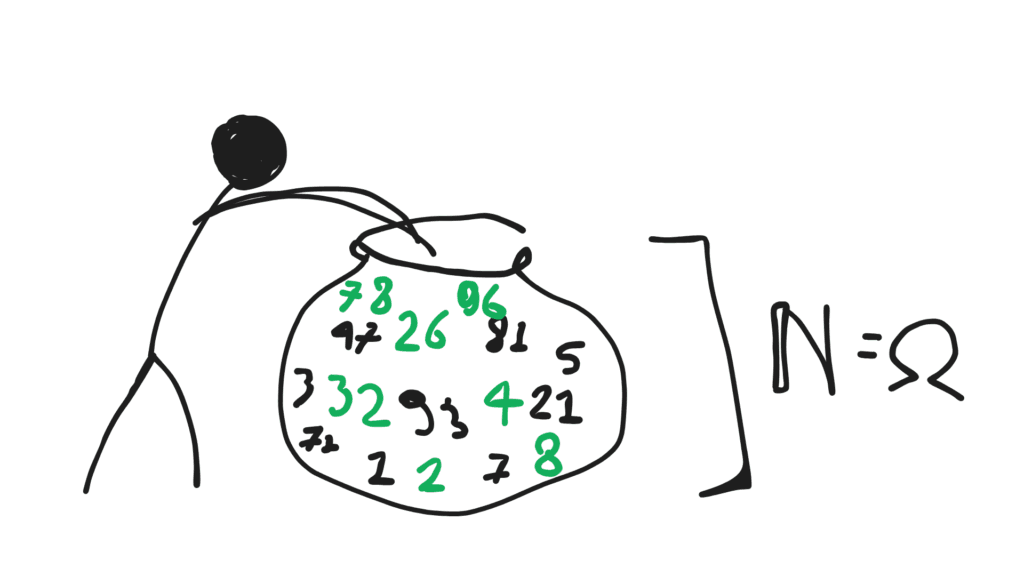
The number of possible cases is ∞ because natural numbers are infinite. But also the number of favorable cases is ∞, like the even numbers in N.
So:
Once again the result does not coincide with the intuition. If we repeat the experiment several times, we expect half E to occur and half not.
The classic probability formula doesn’t help when dealing with infinite quantities.
Example of probabilities
1) Calculate the probability of getting tails when flipping a fair coin.
The number of possible cases is 2, one for heads and one for tails.
Ω = {heads, tails}
|Ω| = 2
The number of favorable cases is just 1, when the outcome is tails.
E = {tails}
|E| = 1
Now we’ve got everything we need.
2. Probability of a dice resulting in a 6
2) Calculate the probability of getting a 6 when rolling a dice.
The number of possible cases is 6, each one for the natural number between 1 – 6.
Ω = {1, 2, 3, 4, 5, 6}
|Ω| = 6
The number of favorable cases is just 1, when the outcome is 6.
E = {tails}
|E| = 1
Now we’ve got everything we need.