Table of Contents
Suppose we have a graph representing the population of a village as a function of time.
Let us take two time instants on the x-axis where the population is equal. Now I ask, when did people live better?
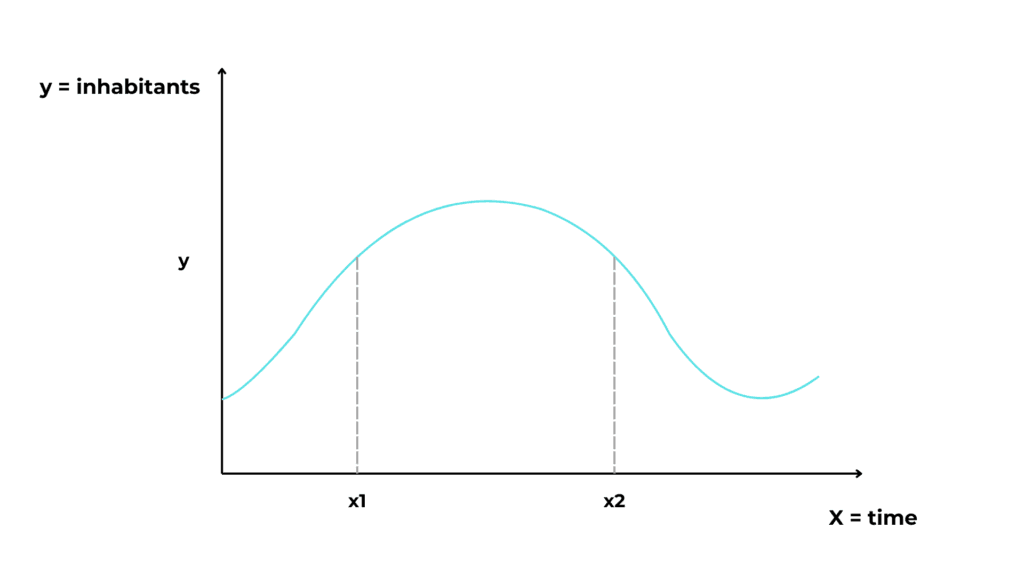
There is no difference between x1 and x2, because the population is the same. But if we move the focus from the absolute y value to the variation of y in our instances, we can see that:
- At point x1 the population was increasing. This means that the people were living well.
- At point x2 the population was decreasing. This means that there may had started a famine or a war.
So when we look at data, the change in a value is important. Is this increasing or decreasing, is it changing slowly or quickly?
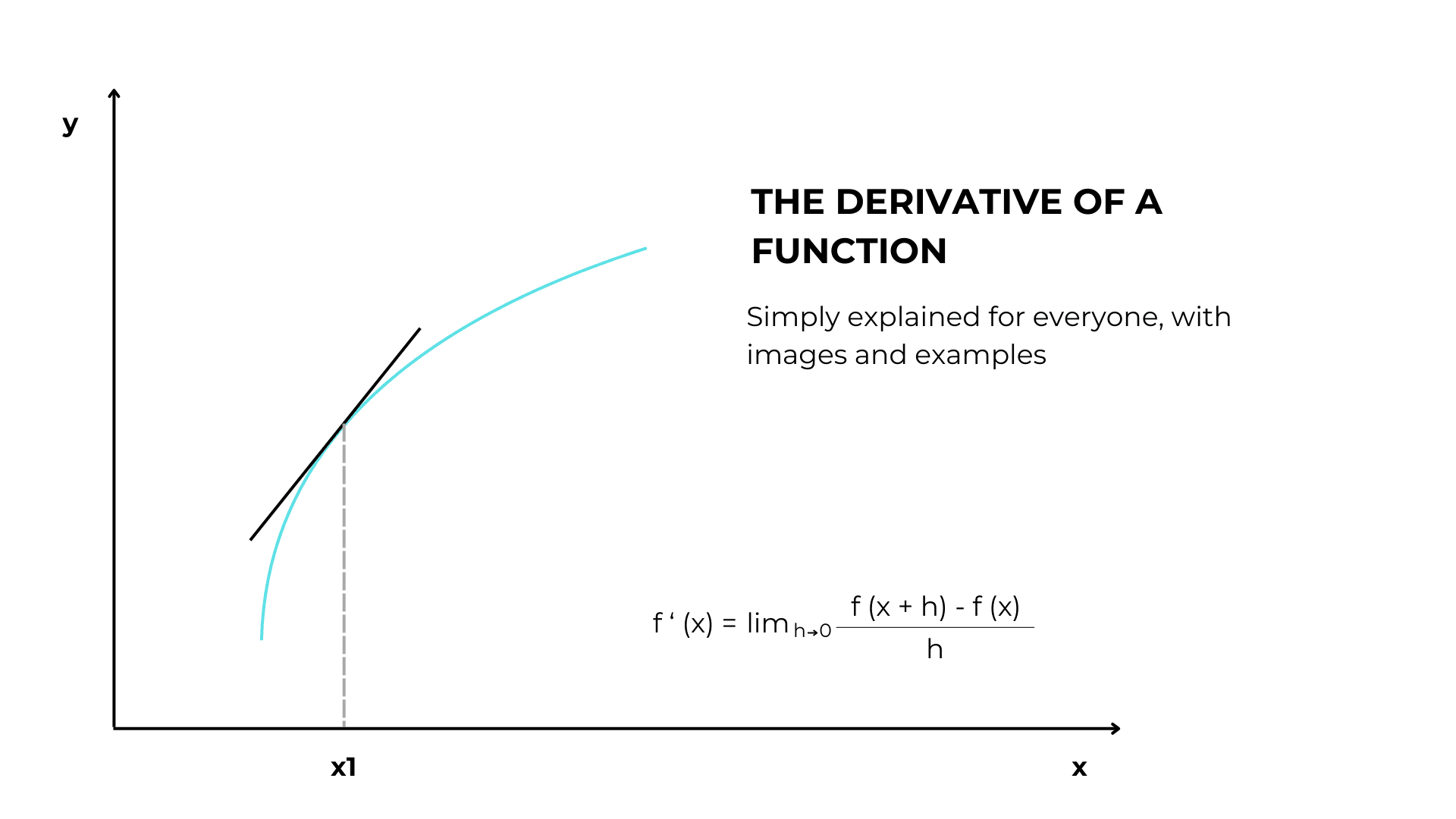
What is the derivative of a function?
The derivative of a function expresses how y changes as x increases.
What is the geometrical meaning of the derivative?
Imagine a function f(x) = 3x.
To find the rate of change of y, we must do a few things:
- Start at a point x1 = 3.
So y1 = 3 ⋅ 3 = 9 - Let x2 be x1 increased by two.
So y2 = 3 ⋅ 5 = 15 - So to find how y change when x increases, we just divide the variation in y to the variation in x.
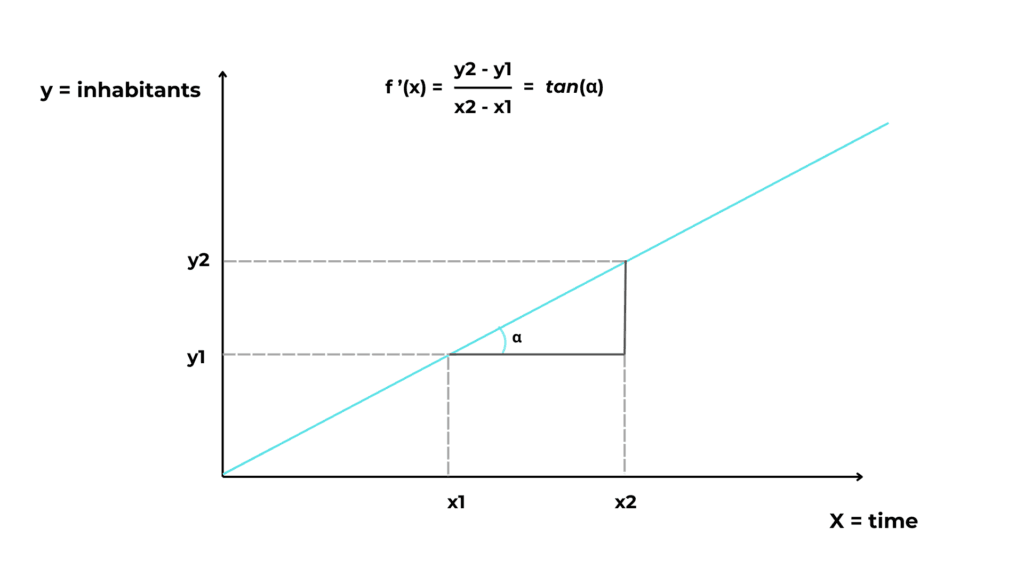
As you can see, our derivative is equal to the slope of the tangent at point x.
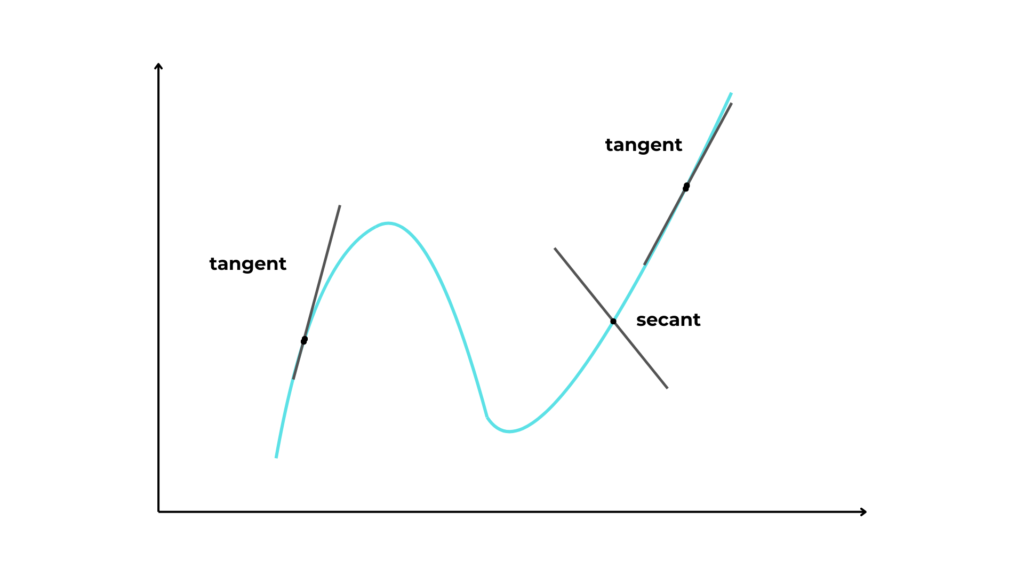
But, what is exactly a tangent?
Given a point x on a curve, the tangent line to x is the line through x and a second point infinitely close to it.
Calculate a derivative: differentiation
Finding the complete formula for the derivative
The tangent line in a linear relationship graphic is easy to find, it’s just the line with the equation.
However, in dealing with curves, we have to start with 4 points, an initial x, an x with a variation h and their relative outputs. We then have to imagine sliding the second point toward x, decreasing h. It’s when h approaches 0 that we have a tangent.
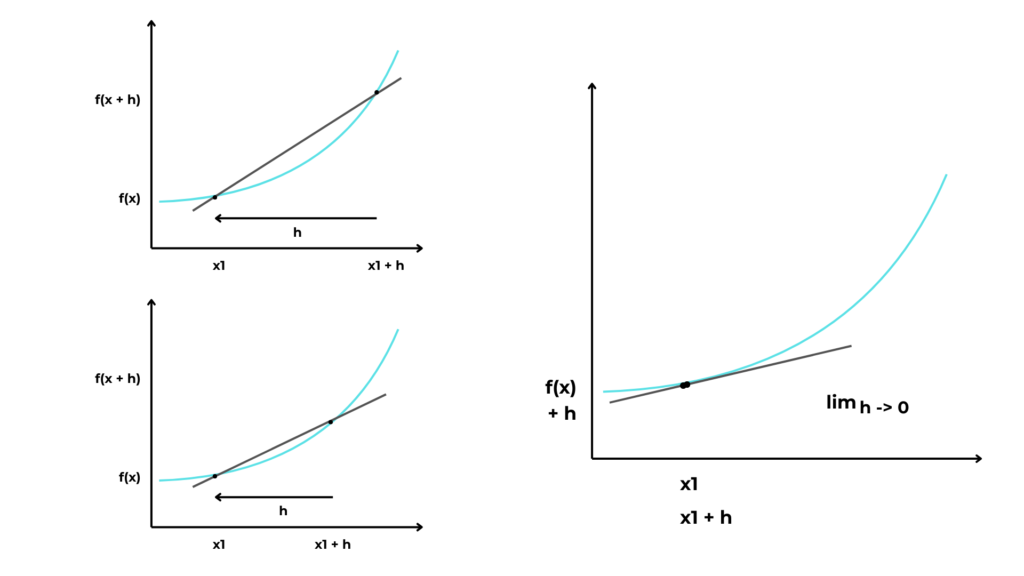
So, the complete formula to find a derivative is:
- Iim(h -> 0) brings h really close to 0
- f(x + h) – f(x) is the variation of y
- h is the variation of x
But what is differentiation?
Differentiation is just the process of calculating the derivative of a function.
Example of differentiation
To solve this problem, we just have apply the formula abov e, where f squares its input.
Shortcuts and rules for differentiation
For our machine learning journey i want you to understand what a derivative is and the meaning it carries. You don’t have to be a mathematical expert or a calculator.
This Wikipedia article explains the shortcuts and rules for differentiation of common functions, you should check it out.
What is a partial derivative?
A partial derivative is the derivative of a multivariate function with respect to one of the variables, while treating the other as costants.
Imagine the function f(x, z) = 3x + z, and we want to calculate the partial derivative with respect to x.
If we treat z as constant, it’s value doesn’t change x ‘s impact on the output.
So the solution is:
What is the gradient of a function?
The gradient of a function, ∇ f, is a vector containing all the partial derivatives of a function.
Why is the derivative important in machine learning?
In machine learning, the derivative is the base of the gradient descent algorithm, used to train many machine learning models.