The derivative of a function explained clearly

Suppose we have a graph representing the population of a village as a function of time.
Let us take two time instants on the x-axis where the population is equal. Now I ask, when did people live better?

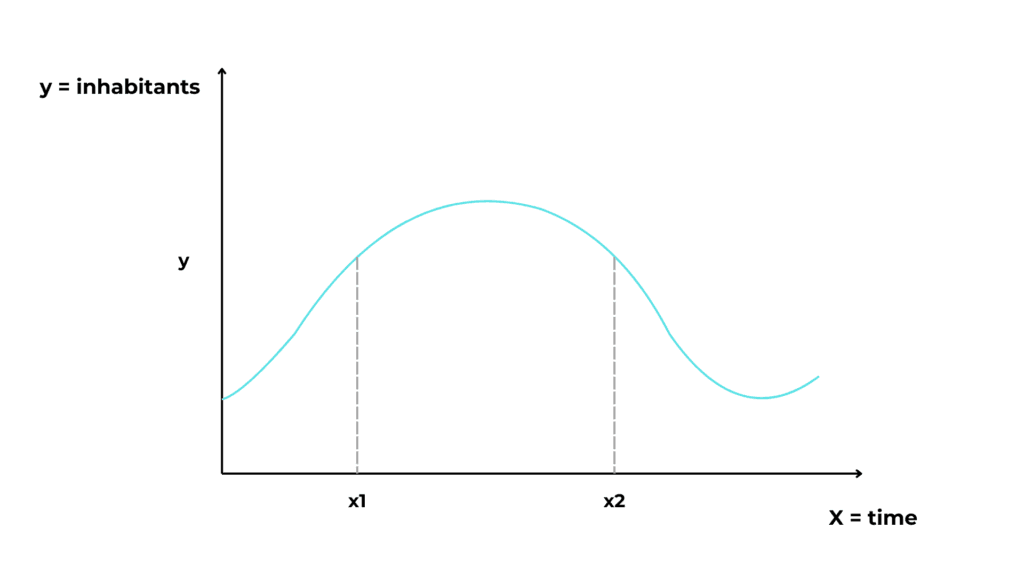
There is no difference between x1 and x2, because the population is the same. But if we move the focus from the absolute y value to the variation of y in our instances, we can see that:

At point x1 the population was increasing. This means that the people were living well.
At point x2 the population was decreasing. This means that there may had started a famine or a war.

So when we look at data, the change in a value is important. Is this increasing or decreasing, is it changing slowly or quickly?

What is the derivative of a function?

The derivative of a function expresses how y changes as x increases.

\[The \; derivative \; notation\; is \; f'(x) \;or \;\frac{df}{dx}\]

What is the geometrical meaning of the derivative?

Imagine a function f(x) = 3x.
To find the rate of change of y, we must do a few things:

Start at a point x1 = 3.
So y1 = 3 ⋅ 3 = 9
Let x2 be x1 increased by two.
So y2 = 3 ⋅ 5 = 15
So to find how y change when x increases, we just divide the variation in y to the variation in x.

\[f'(x) = \frac{Δy}{Δx} = \frac{3 * 2}{2}= 3\]

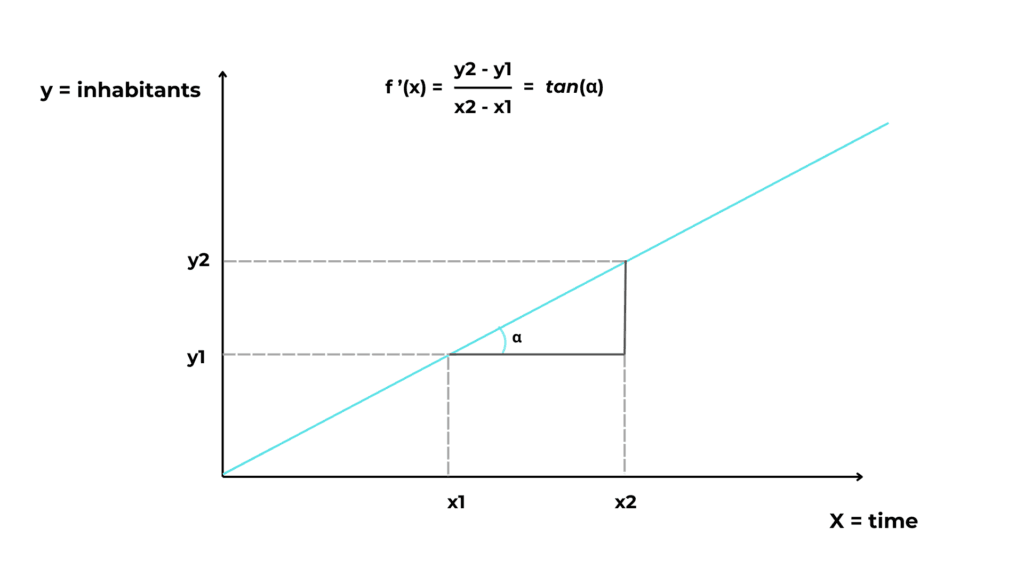
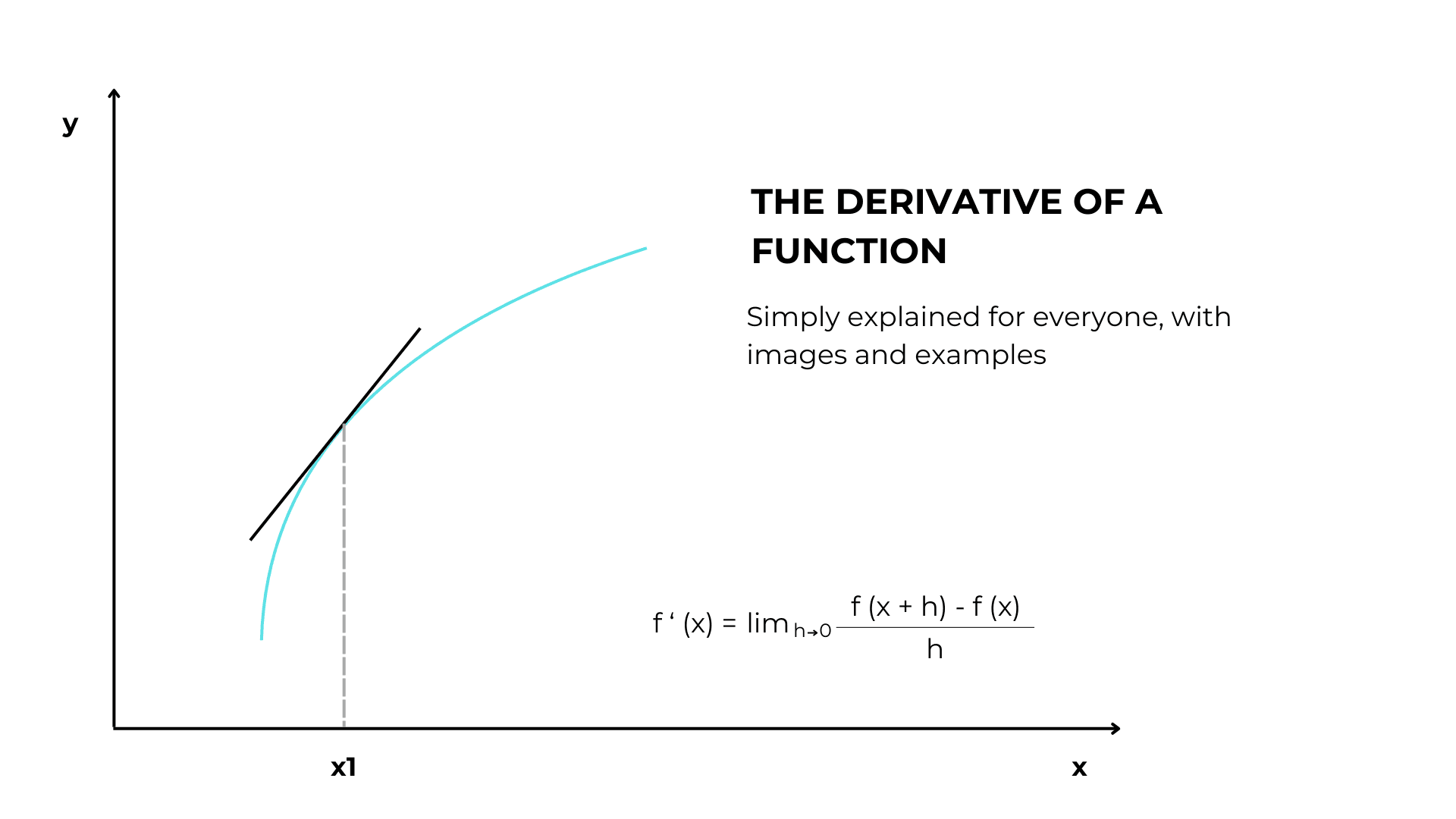
As you can see, our derivative is equal to the slope of the tangent at point x.

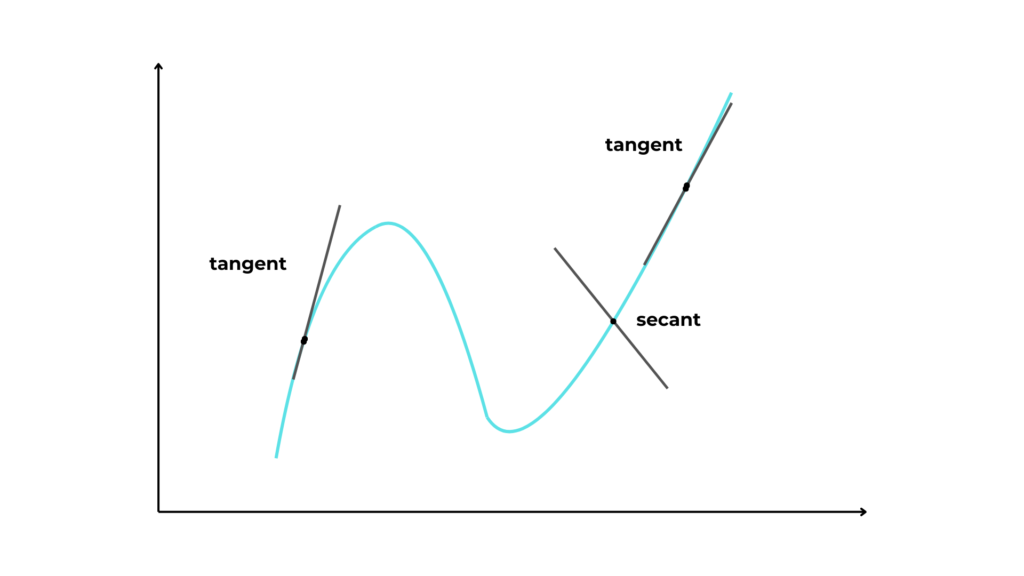
But, what is exactly a tangent?

Given a point x on a curve, the tangent line to x is the line through x and a second point infinitely close to it.

Calculate a derivative: differentiation

Finding the complete formula for the derivative

The tangent line in a linear relationship graphic is easy to find, it’s just the line with the equation.

However, in dealing with curves, we have to start with 4 points, an initial x, an x with a variation h and their relative outputs. We then have to imagine sliding the second point toward x, decreasing h. It’s when h approaches 0 that we have a tangent.

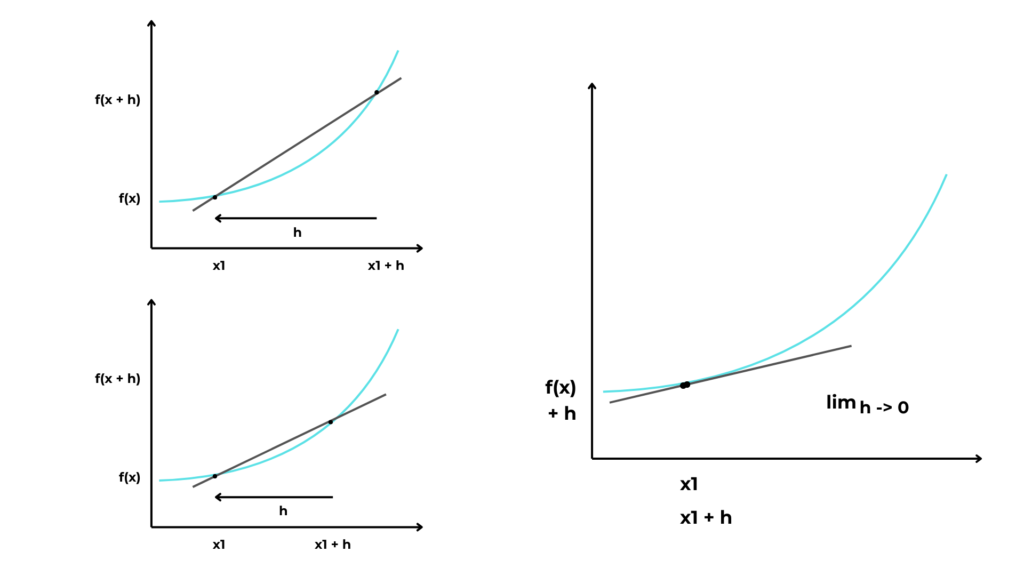
So, the complete formula to find a derivative is:

\[f'(x) = \lim_{h \to 0}\frac{f(x+h) – f(x)}{h}\]

Iim(h -> 0) brings h really close to 0
f(x + h) – f(x) is the variation of y
h is the variation of x

But what is differentiation?

Differentiation is just the process of calculating the derivative of a function.

Example of differentiation

\[f(x) = x^2\]

\[? = f'(x)\]

To solve this problem, we just have apply the formula abov e, where f squares its input.

\[f'(x) = \lim_{h \to 0}\frac{(x + h)^2 – x^2}{h} = \lim_{h \to 0}\frac{2xh + h^2}{h} = \lim_{h \to 0}2x + h = 2x\]

Shortcuts and rules for differentiation

For our machine learning journey i want you to understand what a derivative is and the meaning it carries. You don’t have to be a mathematical expert or a calculator.

This Wikipedia article explains the shortcuts and rules for differentiation of common functions, you should check it out.

What is a partial derivative?

A partial derivative is the derivative of a multivariate function with respect to one of the variables, while treating the other as costants.

\[The \; partial \;derivative \; notation\; is \;\frac{\partial f}{\partial x}\]

Imagine the function f(x, z) = 3x + z, and we want to calculate the partial derivative with respect to x.
If we treat z as constant, it’s value doesn’t change x ‘s impact on the output.
So the solution is:

\[\frac{\partial f}{\partial x} = 3\]

What is the gradient of a function?

The gradient of a function, ∇ f, is a vector containing all the partial derivatives of a function.

Why is the derivative important in machine learning?

In machine learning, the derivative is the base of the gradient descent algorithm, used to train many machine learning models.

Table of Contents